I teach new investors about compound rates of return by employing the Rule of 72. You take a yearly rate of return – say 7% – and divide it into the number 72 to find out how many years it takes to double. So, in this example, an investor receiving a 7% rate of return will see his or her money double in ten years. At 5% a year, an investor will wait 14 years to see their investment double. At 9% a year, they’ll wait just 8 years.
It works backwards too – you can ask “What rate of return must I earn in order to double my money in the next six years and the answer is 72 divided by 6 – you’ll need to compound at 12% for six years in order to get there.
Doubling one’s money throughout their life, multiple times, is the only chance most people have of getting rich. Go look at the entire Forbes 400 list. Everyone on there started a business (or inherited one) and watched its value appreciate over time, doubling and then doubling again and then doubling again. Or the value they recieved from the sale of a business was reinvested into some other venture or real estate or collection or assets that went on to double and then double again. This is how real wealth is created.
Humans are comfortable thinking in terms of incrementalism – I eat a salad every day this week, I lose a few pounds, I do an extra set of pushups each night and I get a little stronger, but doubling is a little harder to conceive of. Especially because of the time necessary for most things to double. Byron Reese writes about humanity’s inability to think in these terms in The Fourth Age:
The fact that technology doubles is a big deal, bigger than one might first suspect. Humans famously underestimate the significance of constant doubling because nothing in our lives behaves that way. You don’t wake up with two kids, then four kids, then eight, then sixteen. Our bank balances don’t go from $100 to $200 to $400 to $800, day after day.
Bank (or portfolio) balances do not adhere to Moore’s Law, doubling in power (or size) every two years. This is good, because if money obeyed the physical law of microchip capacity, we’d be at hyperinflation within a decade. The accumulation of wealth is quiet and steady for most investors, but nevertheless extremely powerful. An investor with a forty year time horizon (between, say, 25 and 65 years of age) could see their money double and double again many times over with a simple portfolio of stock and bond funds. And the best part is that they’re always adding, so that new contributions may only be working on their first double while older contributions may already be on their second or third go-round. Compounding while contributing is fucking beautiful to watch in action, even as it takes place in slow motion.
And the potential is dramatic. This is an amazing illustration and should be seared into your consciousness whenever you think about this topic:
To understand just how quickly something that repeatedly doubles gets really big, consider the story of the invention of chess. About a thousand years ago, a mathematician in what is today India is said to have brought his creation to the ruler, and showed him how the game is played. The ruler, quite impressed, asked the mathematician what he wanted for a reward. The mathematician responded that he was a humble man and his needs were few. He simply asked that a single grain of rice be placed on the first square of the chessboard. Then two on the second, four on the third, each square doubling along the way. All he wanted was the rice that would be on the sixty-fourth square.
So how much rice do you think this is? Given my setup to the story, you know it will be a big number. But just imagine what that much rice would look like. Would it fill a silo? A warehouse? It is actually more rice than has been cultivated in the entire history of humanity. By the way, when the ruler figured this out, he had the mathematician put to death, so there is another life lesson to be learned here.
Reese goes on to explain how dominos lined up, with each one growing progressively larger by 50%, would eventually grow large enough to topple the Empire State Building by the 32nd domino – and that’s only 50% growth. Doubling takes the merely incredible and makes it outright magical.
There are risks to any strategy and the risk to a strategy devoted to long-term compounding is that a lot of the wealth you’re hoping to end up with is meant to be grown toward the end of the period. That final double that happens once you’ve already accumulated quite a bit isn’t a foregone conclusion. In the profession, we call this “sequence of returns risk” and it’s an under-appreciated topic. As Michael Kitces has written, what happens if the investor gets to half a million dollars, having compounded at 8% each year for 30 years, but then the investment climate grows inhospitable for that final ten year stretch – the period in which the $500,000 was supposed to double for the final time, and become a million bucks?
Michael is asking the right question – can financial advisors merely promise doubles by showing a compound interest chart and not spend any time discussing scenarios where that final double fails to materialize in time? Monte Carlo simulations can be helpful here, to show the entire range of outcomes and handicap their likelihood of occurring – but good advice and common sense are even more effective. Instructing clients to “be flexible” and “be conservative” in their expectations and to never put themselves in a position where they “become a forced seller” will also pave the way for a good outcome.
My colleague Ben Carlson wrote about this topic in 2017 and, in my view, he’s done the definitive take on managing sequence of returns risk…
The sequence of the returns matters. The actual S&P 500 returns showed strong performance in the first 10 years, returning more than 310% in total from 1987-1996. The last 10 years have been decent but not nearly as strong, returning roughly 95% in total.
So we’ve looked at three scenarios here that all have the same exact returns but lead to different end results. Here’s the summary:
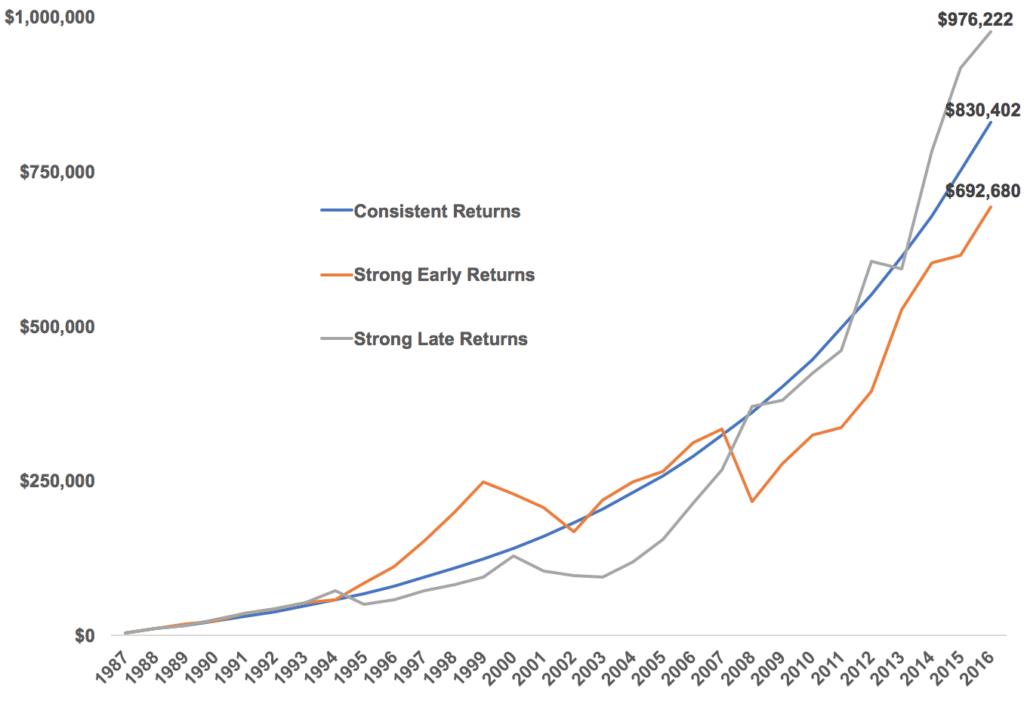
Josh here – like most investors, you don’t get to decide what the sequence of market returns is going to look like over the next ten years or the entirety of your lifetime. Que sera sera. You may end up with better markets earlier in your investing career and worse ones later. This would be unfortunate but not the end of the world. Or you could get lucky, and have a terrible market environment as you’re putting your first decade’s worth of savings to work, followed by an enduring bull market over subsequent decades, which would be the best case scenario.
You can use current valuations to take guesses at what sort of gains the next ten year period may bring – you’ll hear the phrase “expected returns” from people attempting to do this – but the next decade is not guaranteed to look anything like the past, and historical valuation metrics may not remain relevant in the future (just ask the “value-oriented” hedge fund managers who’ve effectively destroyed themselves by short-selling Amazon and Netflix while accumulating JC Penney and Blockbuster over the last 20 years).
You can attempt to outsmart the market each year and manufacture your own rate of return through timing, aggressive trading, superior stock selection, etc, but millions of investors have learned over the years that this is nearly impossible to do, many of them learning the hard way, with massive tax bills, wasted commission dollars and a bottomless hole of missed opportunity, inextinguishable bonfires of regret and the usual war stories told from the edge of a barstool.
On your way to doubling your money, you will face the sequence of returns issue and it’s a legitimate concern. Dealing with questions like these, and building portfolios that have an embedded answer to them, is what we do all day for our clients. And the first thing we tell people is that the mere presence of a potential risk is not a reason to not invest. Risk is why investing pays off in the first place.
Over the last nine years, or 108 months (back to December 2009), the S&P 500 has compounded at a rate of 8.69%. It has doubled your money (111.7%) over this span – the Rule of 72, still functioning ten years after the Great Financial Crisis, imagine that! Actually, it’s much better than that: With dividends reinvested, the S&P 500’s total return to you came out to roughly 10.8% a year or a total compound return of 152% on your money. Now, keep in mind that 2018 was a down year (-5%), while 2011 and 2015 were barely positive (+2% and 1% respectively – only the dividend bailed us out).
And still, during this period investors who woke up, went to work, played with their kids and left their contributed cash in their investment accounts had the ability to earn 150% by doing absolutely nothing. If they had diligently contributed during the 2008-2009 maelstrom, they had that much more to let the miracle of compounding practice its magic upon.
They doubled their money and then some. It was a nice reward after the torment of the Lost Decade, the 2000-2009 period where investors were treated to no such magic and the S&P 500 returned nothing. That’s what they signed up for, whether they knew it or not.
***
This post originally appeared here on January 22nd, 2019
Subscribe to us on YouTube so you never miss an update.




… [Trackback]
[…] Here you will find 5143 additional Info on that Topic: thereformedbroker.com/2019/03/07/double-your-money-2/ […]
… [Trackback]
[…] Read More on that Topic: thereformedbroker.com/2019/03/07/double-your-money-2/ […]
… [Trackback]
[…] Read More to that Topic: thereformedbroker.com/2019/03/07/double-your-money-2/ […]